Data Logger and Telemetry System for Model Airplane – 2, let’s beggin!
Sensors are critically important in the project. The aircraft module collects the data from the sensors and processes it via Arduino mega platform. The system consists of IMU, GPS, temperature, pressure sensors. IMU gives accelerometer, gyro and magnetic compass output.
IMU
An inertial measurement unit, or IMU, is an electronic device that measures and reports on a craft’s velocity, orientation, and gravitational forces, using a combination of accelerometers and gyroscopes, sometimes also magnetometers. IMUs are typically used to maneuver aircraft, including unmanned aerial vehicles (UAVs), among many others, and spacecraft, including shuttles, satellites, and landers [1]. IMU uses accelerometer, gyro, and magnetometer. In this project, each sensor is 3 DOF so the total system has 9 DOF which gives more flexibility in the project.
Accelerometer
Most accelerometers will fall into two categories: digital and analog. Digital accelerometers will give information using a serial protocol like I2C, SPI or USART, while analog accelerometers will output a voltage level within a predefined range that you have to convert to a digital value using an ADC (analog to digital converter) module. In the project, the digital accelerometer is used.
In order to understand the basics of accelerometer, some theories will be discussed. All of the examples are given in the basic form in order to be more explanatory. While this model is not exactly how a MEMS sensor is constructed it is often useful in solving accelerometer related problems. There are actually similar sensors that have metallic balls inside, they are called tilt switches, however they are more primitive and usually they can only tell if the device is inclined within some range or not, not the extent of inclination.
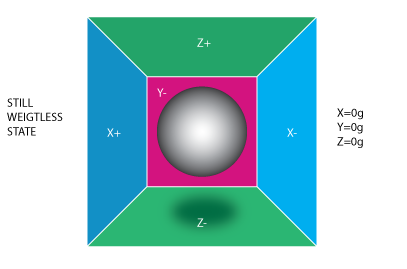
If this box is taken a place with no gravitation fields the ball will simply float in the middle of the box. it can be imagined that the box is in outer-space far-far away from any cosmic bodies, or if such a place is hard to find images at least a spacecraft orbiting around the planet where everything is in a weightless state. From the picture above it can be seen that each axis is assigned to a pair of walls Imagine that each wall is pressure sensitive. If we move suddenly the box to the left (we accelerate it with acceleration 1g = 9.8m/s^2), the ball will hit the wall X-. We then measure the pressure force that the ball applies to the wall and output a value of -1g on the X-axis [2].
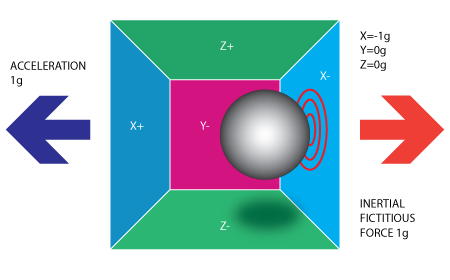
It should be noted that the accelerometer will actually detect a force that is directed in the opposite direction from the acceleration vector. This force is often called Inertial Force or Fictitious Force. One thing you should learn from this is that an accelerometer measures acceleration indirectly through a force that is applied to one of its walls. This force can be caused by the acceleration, but as in the next example, it is not always caused by acceleration [3].
If the example is put into Earth the ball will fall on the Z- wall and will apply a force of 1g on the bottom wall, as shown in the picture below:
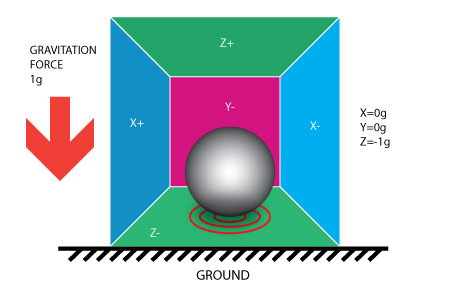
In this case, the box isn’t moving but we still get a reading of -1g on the Z-axis. The pressure that the ball has applied on the wall was caused by a gravitation force.
So far it is analyzed that accelerometer output on a single axis and this is all about a single axis accelerometers. In real life, three-axis accelerometers are used. The real value of triaxial accelerometers comes from the fact that they can detect inertial forces on all three axes. Let’s go back to the box model, and rotate the box 45 degrees to the right. The ball will touch 2 walls now: Z- and X- as shown in the picture below [3]:
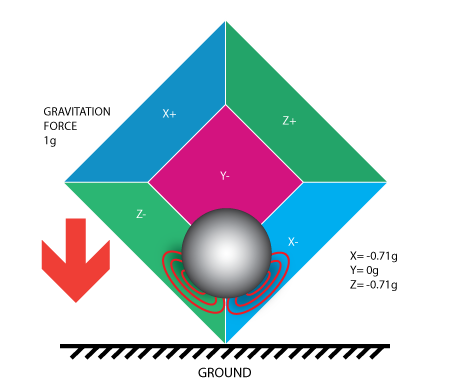
As the degree of freedom of the accelerometer is getting bigger the calculation is getting more complex. Let’s give some basics about the calculation.
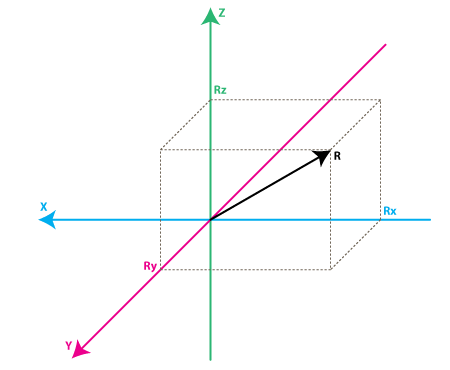
Rx, Ry, Rz are projection of the R vector on the X,Y,Z axes. Please notice the following relation:
| R^2 = Rx^2 + Ry^2 + Rz^2 | (Eq. 1) |
Let’s move on by considering a simple example, suppose our 10bit ADC module gives the following values for the three accelerometer channels (axes)[3]:
Rx = 500
Ry = 600
Rz = 56z
Each ADC module will have a reference voltage, let’s assume in example it is 3.3V. To convert a 10bit adc value to voltage we use the following formula:
| VoltsRx = Rx * Vref / 1023 | (Eq. 2) |
A quick note here: that for 8bit ADC the last divider would be 255 = 2 ^ 8 -1 , and for 12bit ADC last divider would be 4095 = 2^12 -1.
Applying this formula to all 3 channels :
VoltsRx = 500 * 3.3V / 1023 =~ 1.61V
VoltsRy = 600 * 3.3V / 1023 =~ 1.93 V
VoltsRz = 561 * 3.3V / 1023 =~ 1.81V
Each accelerometer has a zero-g voltage level, it can be find in specs, this is the voltage that corresponds to 0g. To get a signed voltage value it is needed to calculate the shift from this level. Let’s say our 0g voltage level is VzeroG = 1.50V. Calculating the voltage shifts from zero-g voltage as follows:
DeltaVoltsRx = 1.61V – 1.5V = 0.11V
DeltaVoltsRy = 1.93V – 1.5V = 0.43V
DeltaVoltsRz = 1.81V – 1.5V = 0.31V
Now accelerometer readings in Volts, it’s still not in g (9.8 m/s^2), to do the final conversion accelerometer sensitivity is applied, usually expressed in mV/g. Let’s say Sensitivity = 478.5mV/g = 0.4785V/g. Sensitivity values can be found in accelerometer specifications. To get the final force values expressed in g we use the following formula:
Rx = DeltaVoltsRx / Sensitivity
Rx = 0.11V / 0.4785V/g =~ 0.23g
Ry = 0.43V / 0.4785V/g =~ 0.88g
Rz = 0.31V / 0.4785V/g =~ 0.65g
Now all 3 components are in the force vector, if the device is not subject to other forces other than gravitation, it can be assumed that this is the direction of the gravitation force vector. If the inclination is wanted to calculate of device relative to the ground the angle between this vector and Z-axis should be calculated. also, the per-axis direction of inclination can be split into 2 components: inclination on the X and Y axis that can be calculated as the angle between the gravitation vector and X / Y axes. Calculating these angles is more simple than thought, now that is calculated the values for Rx, Ry, and Rz.
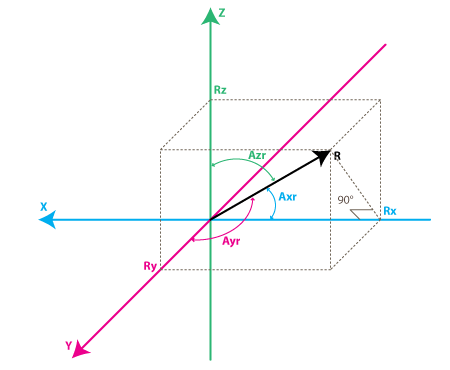
Let’s define angles as Axr, Ayr, Azr. it can be noticed from the right-angle triangle formed by R and Rx that:
cos(Axr) = Rx / R , and similarly :
cos(Ayr) = Ry / R
cos(Azr) = Rz / R
It can be deducted from Eq.1 that R = SQRT( Rx^2 + Ry^2 + Rz^2).
Now our angles can be find by using arccos() function (the inverse cos() function ):
Axr = arccos(Rx/R)
Ayr = arccos(Ry/R)
Azr = arccos(Rz/R)
In this article, we talked about Data Logger and Telemetry System for Model Aircraft. You can reach my other article from the link.
References:
[1] http://en.wikipedia.org/wiki/Inertial_measurement_unit
[2] http://www.starlino.com/imu_guide.html
[3] http://www.instructables.com/id/Accelerometer-Gyro-Tutorial/
